Can The Mass Of An Object Change Without Changing The Amount Of Matter It Has

5 Newton'southward Laws of Motility

5.4 Mass and Weight

Learning Objectives

By the terminate of the department, yous volition be able to:

Explicate the deviation between mass and weight
Explain why falling objects on Earth are never truly in free fall
Describe the concept of weightlessness

Mass and weight are often used interchangeably in everyday chat. For case, our medical records often bear witness our weight in kilograms but never in the right units of newtons. In physics, however, there is an important distinction. Weight is the pull of Earth on an object. It depends on the distance from the center of Earth. Dissimilar weight, mass does not vary with location. The mass of an object is the same on Earth, in orbit, or on the surface of the Moon.

Units of Force

The equation

${F}_{\text{net}}=ma$

is used to define internet force in terms of mass, length, and fourth dimension. As explained earlier, the SI unit of measurement of strength is the newton. Since

${F}_{\text{net}}=ma,$

$1\,\text{N}=1\,\text{kg}·{\text{m/s}}^{2}.$

Although almost the entire world uses the newton for the unit of force, in the United States, the most familiar unit of force is the pound (lb), where 1 N = 0.225 lb. Thus, a 225-lb person weighs grand N.

Weight and Gravitational Force

When an object is dropped, information technology accelerates toward the center of Earth. Newton's second law says that a cyberspace force on an object is responsible for its acceleration. If air resistance is negligible, the net force on a falling object is the gravitational force, normally chosen its weight

$\overset{\to }{w}$

, or its forcefulness due to gravity acting on an object of mass yard. Weight can be denoted as a vector because it has a direction; down is, by definition, the direction of gravity, and hence, weight is a downward force. The magnitude of weight is denoted equally westward. Galileo was instrumental in showing that, in the absence of air resistance, all objects fall with the aforementioned dispatch g. Using Galileo's consequence and Newton's second police, we can derive an equation for weight.

Consider an object with mass grand falling toward Globe. It experiences but the downward forcefulness of gravity, which is the weight

$\overset{\to }{w}$

. Newton's second police force says that the magnitude of the net external force on an object is

${\overset{\to }{F}}_{\text{net}}=m\overset{\to }{a}.$

We know that the acceleration of an object due to gravity is

$\overset{\to }{g},$

$\overset{\to }{a}=\overset{\to }{g}$

. Substituting these into Newton'southward second law gives us the following equations.

Weight

The gravitational force on a mass is its weight. We can write this in vector grade, where

$\overset{\to }{w}$

is weight and one thousand is mass, every bit

$\overset{\to }{w}=m\overset{\to }{g}.$

In scalar course, we can write

$w=mg.$

Since

$g=9.80\,{\text{m/s}}^{2}$

on Globe, the weight of a ane.00-kg object on Earth is nine.80 N:

$w=mg=(1.00\,\text{kg})({9.80\,\text{m/s}}^{2})=9.80\,\text{N}.$

When the net external forcefulness on an object is its weight, we say that it is in costless fall, that is, the only strength acting on the object is gravity. Yet, when objects on World autumn downwards, they are never truly in gratis fall because there is always some upwards resistance strength from the air acting on the object.

Dispatch due to gravity chiliad varies slightly over the surface of Earth, then the weight of an object depends on its location and is non an intrinsic property of the object. Weight varies dramatically if nosotros leave Earth'southward surface. On the Moon, for example, dispatch due to gravity is only

${1.67\,\text{m/s}}^{2}$

. A 1.0-kg mass thus has a weight of ix.8 N on Earth and just about 1.7 North on the Moon.

The broadest definition of weight in this sense is that the weight of an object is the gravitational forcefulness on information technology from the nearest big torso, such as Earth, the Moon, or the Lord's day. This is the most mutual and useful definition of weight in physics. It differs dramatically, however, from the definition of weight used by NASA and the pop media in relation to infinite travel and exploration. When they speak of "weightlessness" and "microgravity," they are referring to the phenomenon we phone call "free fall" in physics. Nosotros use the preceding definition of weight, force

$\overset{\to }{w}$

due to gravity acting on an object of mass m, and we make careful distinctions between gratuitous fall and actual weightlessness.

Be enlightened that weight and mass are different concrete quantities, although they are closely related. Mass is an intrinsic holding of an object: It is a quantity of matter. The quantity or amount of matter of an object is determined by the numbers of atoms and molecules of various types it contains. Because these numbers do not vary, in Newtonian physics, mass does not vary; therefore, its response to an applied forcefulness does not vary. In contrast, weight is the gravitational force acting on an object, so it does vary depending on gravity. For instance, a person closer to the centre of Earth, at a low elevation such as New Orleans, weighs slightly more than than a person who is located in the higher top of Denver, even though they may have the same mass.

It is tempting to equate mass to weight, considering most of our examples have identify on Earth, where the weight of an object varies just a niggling with the location of the object. In addition, it is difficult to count and identify all of the atoms and molecules in an object, so mass is rarely determined in this fashion. If we consider situations in which

$\overset{\to }{g}$

is a constant on Globe, we meet that weight

$\overset{\to }{w}$

is directly proportional to mass chiliad, since

$\overset{\to }{w}=m\overset{\to }{g},$

that is, the more massive an object is, the more information technology weighs. Operationally, the masses of objects are determined by comparison with the standard kilogram, as we discussed in Units and Measurement. Simply by comparing an object on Earth with one on the Moon, we tin can easily run into a variation in weight but not in mass. For instance, on Globe, a five.0-kg object weighs 49 N; on the Moon, where g is

${1.67\,\text{m/s}}^{2}$

, the object weighs 8.iv Due north. However, the mass of the object is still 5.0 kg on the Moon.

Case

Clearing a Field

A farmer is lifting some moderately heavy rocks from a field to establish crops. He lifts a rock that weighs 40.0 lb. (well-nigh 180 North). What force does he employ if the stone accelerates at a charge per unit of

$1.5\,{\text{m/s}}^{2}?$

Strategy

We were given the weight of the stone, which we use in finding the net force on the rock. Nevertheless, we also need to know its mass to utilize Newton's second law, so we must apply the equation for weight,

$w=mg$

, to determine the mass.

Solution

No forces act in the horizontal direction, and so we can concentrate on vertical forces, every bit shown in the following free-body diagram. We label the dispatch to the side; technically, it is not part of the free-body diagram, but it helps to remind u.s.a. that the object accelerates upward (so the internet force is upward).

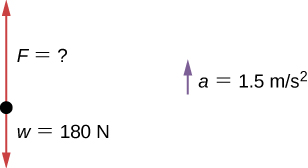
Figure shows a free-body diagram with vector w equal to 180 newtons pointing downwards and vector F of unknown magnitude pointing upwards. Acceleration a is equal to 1.5 meters per second squared. — $\begin{array}{ccc}\hfill w& =\hfill & mg\hfill \\ \hfill m& =\hfill & \frac{w}{g}=\frac{180\,\text{N}}{9.8\,{\text{m/s}}^{2}}=18\,\text{kg}\hfill \\ \hfill \sum F& =\hfill & ma\hfill \\ \hfill F-w& =\hfill & ma\hfill \\ \hfill F-180\,\text{N}& =\hfill & (18\,\text{kg})(1.5\,{\text{m/s}}^{2})\hfill \\ \hfill F-180\,\text{N}& =\hfill & 27\,\text{N}\hfill \\ \hfill F& =\hfill & 207\,\text{N}=210\,\text{N to two significant figures}\hfill \end{array}$

\[\begin{array}{ccc}\hfill w& =\hfill & mg\hfill \\ \hfill m& =\hfill & \frac{w}{g}=\frac{180\,\text{N}}{9.8\,{\text{m/s}}^{2}}=18\,\text{kg}\hfill \\ \hfill \sum F& =\hfill & ma\hfill \\ \hfill F-w& =\hfill & ma\hfill \\ \hfill F-180\,\text{N}& =\hfill & (18\,\text{kg})(1.5\,{\text{m/s}}^{2})\hfill \\ \hfill F-180\,\text{N}& =\hfill & 27\,\text{N}\hfill \\ \hfill F& =\hfill & 207\,\text{N}=210\,\text{N to two significant figures}\hfill \end{array}\] — $\begin{array}{ccc}\hfill w& =\hfill & mg\hfill \\ \hfill m& =\hfill & \frac{w}{g}=\frac{180\,\text{N}}{9.8\,{\text{m/s}}^{2}}=18\,\text{kg}\hfill \\ \hfill \sum F& =\hfill & ma\hfill \\ \hfill F-w& =\hfill & ma\hfill \\ \hfill F-180\,\text{N}& =\hfill & (18\,\text{kg})(1.5\,{\text{m/s}}^{2})\hfill \\ \hfill F-180\,\text{N}& =\hfill & 27\,\text{N}\hfill \\ \hfill F& =\hfill & 207\,\text{N}=210\,\text{N to two significant figures}\hfill \end{array}$

Significance

To apply Newton's second law as the master equation in solving a problem, we sometimes have to rely on other equations, such every bit the one for weight or one of the kinematic equations, to consummate the solution.

Bank check Your Understanding

For (Case), find the acceleration when the farmer's applied force is 230.0 North.

[reveal-answer q="fs-id1165036763010″]Show Solution[/reveal-answer]

[hidden-respond a="fs-id1165036763010″]

$a=2.78\,{\text{m/s}}^{2}$

[/hidden-answer]

Tin you avoid the bedrock field and state safely but before your fuel runs out, equally Neil Armstrong did in 1969? This version of the classic video game accurately simulates the real move of the lunar lander, with the correct mass, thrust, fuel consumption rate, and lunar gravity. The real lunar lander is hard to control.

Use this interactive simulation to move the Lord's day, Earth, Moon, and space station to meet the effects on their gravitational forces and orbital paths. Visualize the sizes and distances betwixt different heavenly bodies, and plow off gravity to see what would happen without it.

Summary

Mass is the quantity of affair in a substance.
The weight of an object is the net force on a falling object, or its gravitational force. The object experiences acceleration due to gravity.
Some upward resistance forcefulness from the air acts on all falling objects on Globe, then they can never truly be in free fall.
Careful distinctions must be made between free fall and weightlessness using the definition of weight every bit force due to gravity acting on an object of a certain mass.

Conceptual Questions

What is the relationship between weight and mass? Which is an intrinsic, unchanging holding of a trunk?

How much does a seventy-kg astronaut weight in space, far from any celestial body? What is her mass at this location?

[reveal-respond q="fs-id1165038279773″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1165038279773″]

The astronaut is truly weightless in the location described, because there is no large body (planet or star) nearby to exert a gravitational strength. Her mass is seventy kg regardless of where she is located.

[/hidden-respond]

Which of the post-obit statements is accurate?

(a) Mass and weight are the aforementioned thing expressed in different units.

(b) If an object has no weight, it must have no mass.

(d) Mass and inertia are different concepts.

(e) Weight is always proportional to mass.

When you stand on Earth, your anxiety push button against information technology with a force equal to your weight. Why doesn't Earth accelerate away from you?

[reveal-respond q="fs-id1165038186995″]Show Solution[/reveal-answer]

[hidden-answer a="fs-id1165038186995″]

The strength you exert (a contact strength equal in magnitude to your weight) is small-scale. Earth is extremely massive by comparison. Thus, the acceleration of World would be incredibly pocket-size. To see this, use Newton'due south second law to summate the acceleration yous would cause if your weight is 600.0 North and the mass of Earth is

$6.00\,×\,{10}^{24}\,\text{kg}$

.
[/hidden-answer]

How would you lot give the value of

$\overset{\to }{g}$

in vector course?

Problems

The weight of an astronaut plus his infinite arrange on the Moon is only 250 North. (a) How much does the suited astronaut counterbalance on Globe? (b) What is the mass on the Moon? On World?

[reveal-answer q="fs-id1165038377147″]Bear witness Solution[/reveal-reply]

[hidden-answer a="fs-id1165038377147″]

$\begin{array}{ccc}\hfill {w}_{\text{Moon}}& =\hfill & m{g}_{\text{Moon}}\hfill \\ \hfill m& =\hfill & 150\,\text{kg}\hfill \\ \hfill {w}_{\text{Earth}}& =\hfill & 1.5\,×\,{10}^{3}\,\text{N}\hfill \end{array}$

; b. Mass does not alter, so the suited astronaut'southward mass on both Globe and the Moon is

$150\,\text{kg.}$

[/subconscious-respond]

Suppose the mass of a fully loaded module in which astronauts accept off from the Moon is

$1.00\,×\,{10}^{4}$

kg. The thrust of its engines is

$3.00\,×\,{10}^{4}$

N. (a) Calculate the module'southward magnitude of acceleration in a vertical takeoff from the Moon. (b) Could information technology lift off from Earth? If not, why not? If information technology could, calculate the magnitude of its dispatch.

A rocket sled accelerates at a rate of

${49.0\,\text{m/s}}^{2}$

. Its passenger has a mass of 75.0 kg. (a) Calculate the horizontal component of the force the seat exerts against his torso. Compare this with his weight using a ratio. (b) Calculate the direction and magnitude of the total forcefulness the seat exerts against his torso.

[reveal-answer q="fs-id1165038050933″]Show Solution[/reveal-answer]

[hidden-respond a="fs-id1165038050933″]

$\begin{array}{ccc}\hfill {F}_{\text{h}}& =\hfill & 3.68\,×\,{10}^{3}\,\text{N and}\hfill \\ \hfill w& =\hfill & 7.35\,×\,{10}^{2}\,\text{N}\hfill \\ \hfill \frac{{F}_{\text{h}}}{w}& =\hfill & 5.00\,\text{times greater than weight}\hfill \end{array}$

;
b.

$\begin{array}{ccc}\hfill {F}_{\text{net}}& =\hfill & 3750\,\text{N}\hfill \\ \hfill \theta & =\hfill & 11.3\text{°}\,\text{from horizontal}\hfill \end{array}$

[/subconscious-answer]

Echo the previous trouble for a situation in which the rocket sled decelerates at a charge per unit of

${201\,\text{m/s}}^{2}$

. In this problem, the forces are exerted by the seat and the seat belt.

A body of mass ii.00 kg is pushed straight upward by a 25.0 N vertical force. What is its acceleration?

[reveal-answer q="fs-id1165038013723″]Bear witness Solution[/reveal-answer]

[hidden-answer a="fs-id1165038013723″]

$\begin{array}{ccc}\hfill w& =\hfill & 19.6\,\text{N}\hfill \\ \hfill {F}_{\text{net}}& =\hfill & 5.40\,\text{N}\hfill \\ \hfill {F}_{\text{net}}& =\hfill & ma⇒a=2.70\,{\text{m/s}}^{2}\hfill \end{array}$

[/subconscious-reply]

A car weighing 12,500 N starts from rest and accelerates to 83.0 km/h in v.00 south. The friction force is 1350 Due north. Discover the applied force produced by the engine.

A body with a mass of 10.0 kg is causeless to be in Earth's gravitational field with

$g=9.80\,{\text{m/s}}^{2}$

. What is its acceleration?

[reveal-reply q="fs-id1165036901240″]Bear witness Solution[/reveal-reply]

[hidden-answer a="fs-id1165036901240″]

$0.60\hat{i}-8.4\hat{j}\,{\text{m/s}}^{2}$

[/hidden-answer]

A firefighter has mass m; he hears the fire warning and slides down the pole with acceleration a (which is less than g in magnitude). (a) Write an equation giving the vertical forcefulness he must employ to the pole. (b) If his mass is 90.0 kg and he accelerates at

$5.00\,{\text{m/s}}^{2},$

what is the magnitude of his applied force?

A baseball catcher is performing a stunt for a telly commercial. He will catch a baseball (mass 145 thou) dropped from a summit of 60.0 m in a higher place his glove. His glove stops the ball in 0.0100 s. What is the force exerted past his glove on the brawl?

[reveal-reply q="fs-id1165038336069″]Prove Solution[/reveal-answer]

[hidden-answer a="fs-id1165038336069″]

497 Northward

[/hidden-answer]

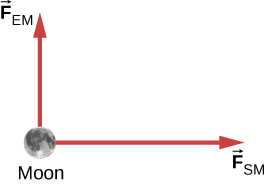
When the Moon is directly overhead at sunset, the force past Earth on the Moon,

${F}_{\text{EM}}$

, is substantially at

$90\text{°}$

to the force by the Sun on the Moon,

${F}_{\text{SM}}$

, equally shown beneath. Given that

${F}_{\text{EM}}=1.98\,×\,{10}^{20}\,\text{N}$

and

${F}_{\text{SM}}=4.36\,×\,{10}^{20}\,\text{N},$

all other forces on the Moon are negligible, and the mass of the Moon is

$7.35\,×\,{10}^{22}\,\text{kg},$

make up one's mind the magnitude of the Moon'southward acceleration.
Figure shows a circle labeled moon. An arrow from it, pointing up is labeled F subscript EM. Another arrow from it pointing right is labeled F subscript SM.

Glossary

free fall: state of affairs in which the only strength acting on an object is gravity

weight

force

$\overset{\to }{w}$

due to gravity acting on an object of mass m

Source: https://opentextbc.ca/universityphysicsv1openstax/chapter/5-4-mass-and-weight/

Posted by: woodsfambireett.blogspot.com

Can The Mass Of An Object Change Without Changing The Amount Of Matter It Has

5.4 Mass and Weight

Learning Objectives

Units of Force

Weight and Gravitational Force

Weight

Case

Clearing a Field

Strategy

Solution

Significance

Bank check Your Understanding

Summary

Conceptual Questions

Problems

Glossary

0 Response to "Can The Mass Of An Object Change Without Changing The Amount Of Matter It Has"

Post a Comment

Iklan Atas Artikel

Iklan Tengah Artikel 1

Iklan Tengah Artikel 2

Iklan Bawah Artikel